设计是一项具有挑战性的任务,涉及线性度、效率、增益和输出功率之间的权衡。在这里,我们研究共发射极电路如何能够或不能用作
本系列之前的文章讨论了小信号放大器,它通常设计用于增益和线性,而不是功率传输。如果接下来的电路具有纯电容输入阻抗,则小信号放大器可能会提供特定的电压或电流增益,而不会向实际负载传输任何明显的功率。由于小信号放大器不处理高功率电平,因此功率解决能力和功率效率也不是其主要设计要求。
在接下来的几篇文章中,我们将讨论一些截然不同的内容:射频功率放大器功率放大器(PA)出现在发射机的输出端,负责将射频功率传输到天线。我们大家可以预计功率放大器的峰值交流电流在200毫安或更高的范围内——当然并非是小信号。
这让我们区分了功率放大器和线性小信号放大器的重要区别。功率放大器的交流电流通常与其静态偏置电流相当。由于功率放大器处理大量的交流电流,而大偏置电流意味着线性操作较差,因此我们大家可以预期功率放大器绝大多数都是非线性的。即使是A类功率放大器——最线性的功率放大器类型,也是本文的主要主题——通常被设计为提供等于晶体管偏置电流的峰值交流电流。
我们将通过检查功率效率和功率解决能力的问题来开始我们对A类功率放大器的研究,这两者在PA设计中都是最重要的。然后我们将看看我们是不是可以通过使用共发射极级作为功率放大器来解决这些问题。在我们完成一些计算后,我们将介绍电感负载的A类功率放大器。
由于它们旨在提供大量的输出功率,因此功率放大器是射频收发器中最耗电的模块。例如,如果向天线 kW功率的功率放大器效率仅为50%,则放大器本身将消耗30 kW。这可能是一个相当具有挑战性的热管理问题。
效率是一个主要问题,无论PA是向广播发射机的天线提供数十瓦的功率,还是向便携式通信设备的天线提供几瓦的功率。即使在低功耗的便携式应用中,低效率的PA在产生可用输出功率方面效率较低——事实上,PA会浪费电池提供的可用功率。使用更高效的PA,电池供电设备的使用时间可以更长。
另一个PA设计挑战来自大型信号功率放大器通常要处理的问题。考虑一个向50Ω天线W射频功率的便携式设备。这需要提供20V的峰峰电压摆幅和200mA的峰值电流通过天线。正如你所看到的,即使在这种低功率应用中,晶体管也必须处理高压和电流水平,以在输出端提供所需数量的射频功率。
同时,在高功率应用中,有源器件必须处理远高于此的电压和电流。晶体管在它们可以处理的最大电压和电流水平方面以及在不损坏的情况下可以燃烧的最大功率方面都受到限制,因此这可能是有问题的。
让我们研究一下使用共发射极(或共源极)级作为功率放大器的可能性。我们能否利用足够大的晶体管来有效地提供大量的输出功率?假设图1中所示的共发射极级向50Ω负载电阻(RL)提供1W的功率。
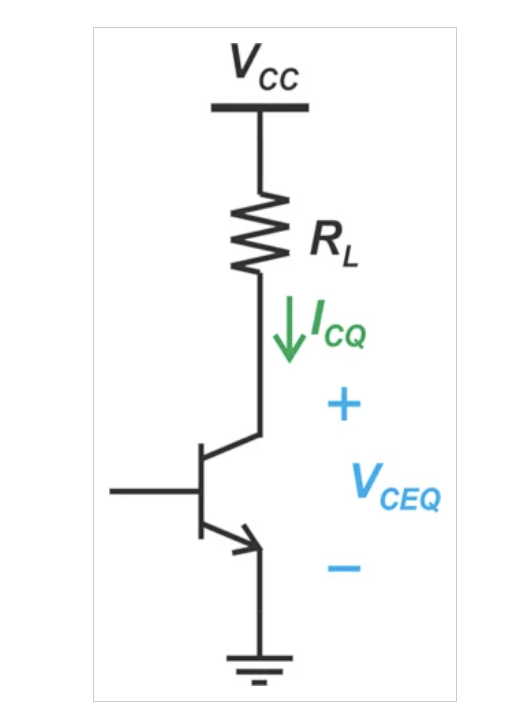
为了将图1中的电路用作PA,我们显然需要用能够耗散几瓦到几十瓦而不被损坏的功率晶体管。然而,最要紧的麻烦仍然是如何最大化电路的输出功率。
负载的电压和电流的乘积决定了输送的功率。为实现最大输出功率,应选择偏置点以最大化负载的电压和电流摆动。当晶体管被偏置在其有源区的中间时,实现最大摆动。为了找到比较合适的偏置点,我们为集电极支路写了一个KVL方程:
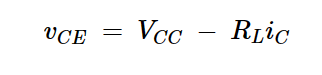
该方程式给出了电路的交流负载线所示。任何可能的iC值和相应的vCE值都落在交流负载线上。
共射极放大器的交流负载线:共发射极电路的交流负载线。偏置点(ICQ和VCEQ)可以在两条虚线的交点处找到。
在我们的简单示例中,交流和直流负载线是相同的。这使得确定电压和电流限制变得容易——当晶体管处于截止状态(iC = 0)时,整个电源电压因此出现在集电极和发射极端子之间(vCE = VCC)。另一方面,对于饱和晶体管,集电极和发射极端子之间会出现非常小的电压降(通常为0.1 V)。忽略这个很小的电压降,我们找到了集电极电流的最大值:
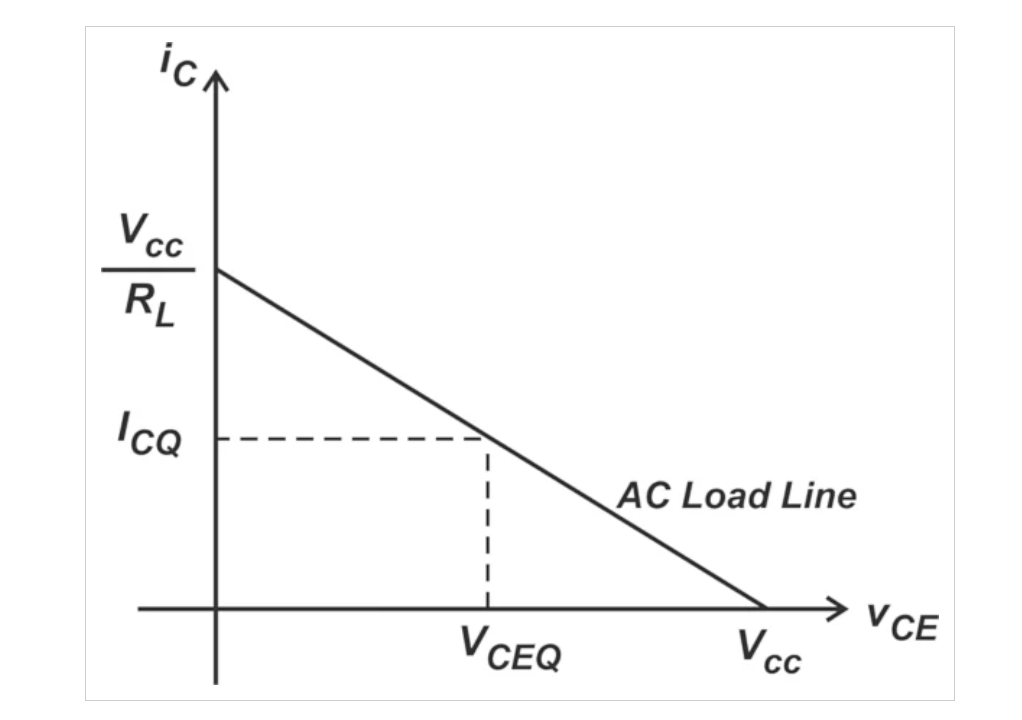
交流负载线显示了电路中的电流和电压限制。通过将所采用特定类型的晶体管(BJT、FET等)的特性曲线叠加在交流负载线上,我们大家可以很容易地确定信号何时超过晶体管的线性范围。
换句话说,在最大输出功率的情况下,我们大家可以假设集电极电流由ICQ的偏置电流和振幅为ic,max的正弦电流分量组成:
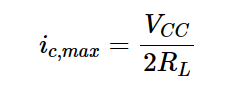
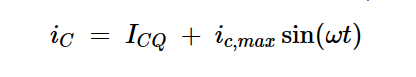
传递给负载的功率有两个组成部分:来自偏置电流的直流功率和我们大家都希望最大化的交流功率。由于我们大家都知道集电极的峰值交流电流(ic,max),我们大家可以计算传递给负载的交流功率的平均值,如下式所示:
请注意,这是负载的最大交流功率。当交流信号不存在时,向负载提供的交流功率为零。
这意味着电源必须要提供4 W才能向负载提供1 W。额外的3 W的一部分在晶体管中损失;其余部分作为RL中的直流功率损失。在实践中,可实现的效率可能远低于25%。
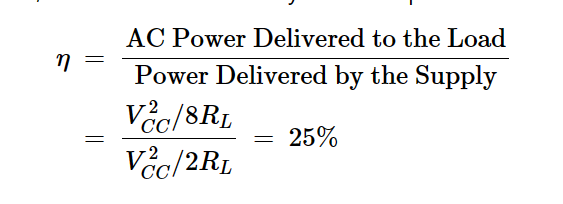
假设电源电压VCC=12V,静态电流ICQ=0.75A,RL的值是多少才能产生最大的输出功率?
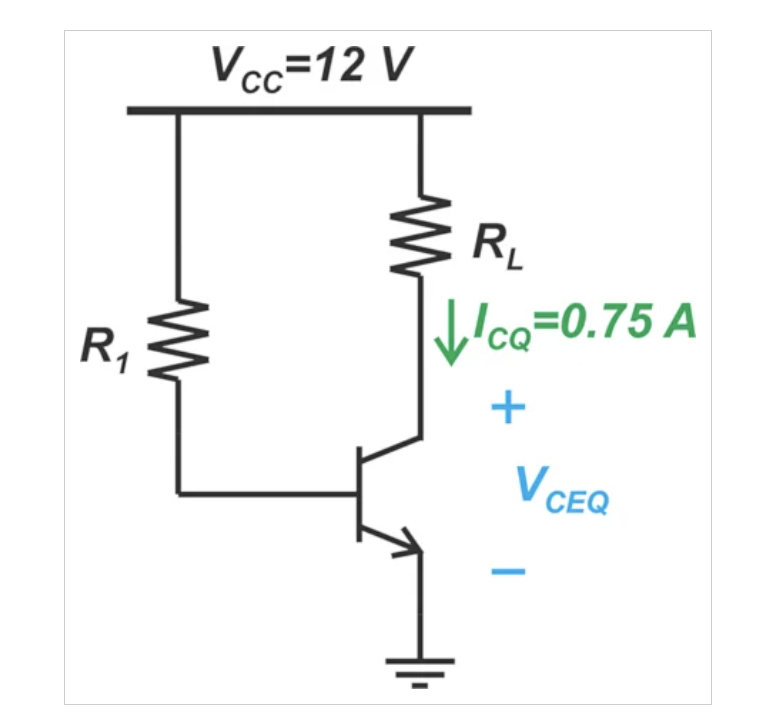
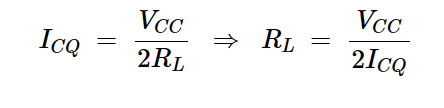
图4显示了三个不同负载电阻值的负载线 Ω。该图让我们直观地了解给定静态电流的不同负载电阻怎么样产生不同的电压波动,由此产生不同的输出功率值。
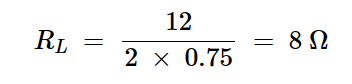
图4.三个不同负载电阻值的负载线 Ω(紫色),RL = 8 Ω(蓝色),RL = 13.33 Ω(橙色)。


